M a 1 2 2 c 2 2 b 2 a 2. In this regard what is the formula for median of a triangle.

Triangle Centers Posters Points Of Concurrency Math Posters High School Free Math Lessons Secondary Math
The centroid divides the medians segments in a ratio.

Formula for median of triangle. The medians are concurrent at the centroid. In the figure shown below the median from A meets the mid-point of the opposite side BC at point D. So for a data set 3 5 7 9 11 7 is the median.
Stewarts Theorem applied to the case gives the length of the median. Find the length of height bisector median if given all side L. Therefore the ratio of the areas of triangle AFC to FHC is 4 to 3 and so the ratio of the area of triangle ABC to CGF is 4 to 3.
In geometry a median of a triangle is a line segment joining a vertex to the midpoint of the opposite side thus bisecting that side. Use Herons formula for the area of the triangle with sides of length u v and w. Displaystyle m_a frac 1 2sqrt 2c22b2-a2 ma.
Lets denote the medians by m a m b m c and the triangle sides by a b c. What is the formula for median of a triangle. Formula for the median of a triangle in terms of the length of the sides.
Hence AD is the median of ABC and it bisects the side BC into two halves where BD BC. A median of a triangle is a line segment joining a vertex to the midpoint of the opposite side thus bisecting that side. It is a bit wordy but can be translated into a formula.
Each triangle has medians. Every triangle has exactly three medians one from each vertex and they all intersect each other at the triangles centroidIn the case of isosceles and equilateral triangles a median bisects any angle at a vertex whose two adjacent sides are equal in length. The length of the median drawn to a side of a triangle is equal to one half the square root of the double product of the sum of the squares of the lengths of the two other sides minus the squared length of this side.
Because a triangle has three vertexes it also has three medians. A median of a triangle is a line segment that goes from one of a triangles three vertexes to the midpoint of the opposite side. Find the length of height bisector median if given equal sides and angle formed by the equal sides L.
How to Find the Equation of the Median of a Triangle. In a right triangle five multiplied by the square of the length of the median drawn to the hypotenuse is equal to the sum of the squares of the lengths of the medians drawn to the legs. The mathematical word median has different meanings with different operations.
A 9 B 12 C 15. In statistics it is the value lying at the midpoint of a data set. A median of a triangle is a line segment drawn from a vertex to the midpoint of the opposite side of the vertex.
A median of a triangle is the line segment that joins any vertex of the triangle with the mid-point of its opposite side. Substituting and simplifying leads to the result. The formula for the median of a triangle is given by using Apolloniuss Theorem ma 2b22c2a2 4 m a 2 b 2 2 c 2 a 2 4 where a b c are the sides of the triangle ma is the length of the median from vertex A.
Apolloniuss Theorem states that in any triangle the sum of the squares on any two sides is equal to twice the square on half the third side together with twice the square on the median which bisects the third side. Find the length of height bisector median if given side base and angle at the base L. For a given triangle the second median divides the triangle formed by the first median in the ratio 12.
It is a bit wordy but can be translated into a formula. The point of concurrency is called the centroid. The median of a triangle further divides the triangle into two triangles having the exact area measurement.
The medians of a triangle are concurrent at a point. Median in a right triangle. The area of the triangle with medians of length u v and w is.
Using Apolloniuss Theorem the formula for the median of a triangle is given by m a 2 b 2 2 c 2 a 2 4 sqrtfrac2b22c2-a24 4 2 b 2 2 c 2 a 2 where a b c are the sides of the triangle and m a is the length of the median from the vertex A. In geometry a median is a line segment from an interior angle of a triangle to the midpoint of the opposite side.

Image Result For Orthocenter Centroid Circumcenter And Incenter Triangle Worksheet Geometry Worksheets Plane Geometry

Ncert Solutions For Class 10 Maths Chapter 7 Coordinate Geometry Ex 7 3 Cbsetuts Com Ch7mathsclass10 Math Coordinate Geometry Chapter

Median Of A Triangle Geometry Math Dictionary Math Geometry Geometry High School Teaching Geometry

Pin On Geometry Theorems And Problems Math

Midsegments And Medians Of Triangles Midsegment Theorem And Median Theorem Practice Worksheet For High Triangle Worksheet Word Problem Worksheets Worksheets

Mathformula Formula Apollonius Theorem Via Degreefromcanada

Median Don Steward Mathematics Teaching Biggest Square Inside A Right Angled Triangle Math Methods Math Geometry Teaching Math

Perimeter And Circumference 1 In 2021 Area And Perimeter Math Practices Area Of A Circle

Special Lines In A Triangle Math Help Triangle Math Interior And Exterior Angles Geometry Problems

Geometry Problem 1296 Heron S Formula Area Of Triangle In Terms Of The Medians School College Geometry Sat Prep Sat Prep Geometry Problems Geometry

Triangle Concurrency Abmp Oicc Abmp Triangle Acute Triangle

Pythagorean Theorem And Right Triangle Formulas Plane Geometry College Elearning Plane Geometry Triangle Formula Right Triangle

Chart Shows Basic Geometry Formulas And Definitions For Area And Perimeter Back Of Chart Features Reproducible Area And Perimeter Studying Math Learning Math

Theorems Similar Triangles Right Triangle

Pin On Geometry Theorems And Problems Math

Geometry Problem 153 Circumscribed Quadrilateral Diagonals Concurrent With Chords School College Math Educatio Geometry Problems Math Tutorials Math Tutor
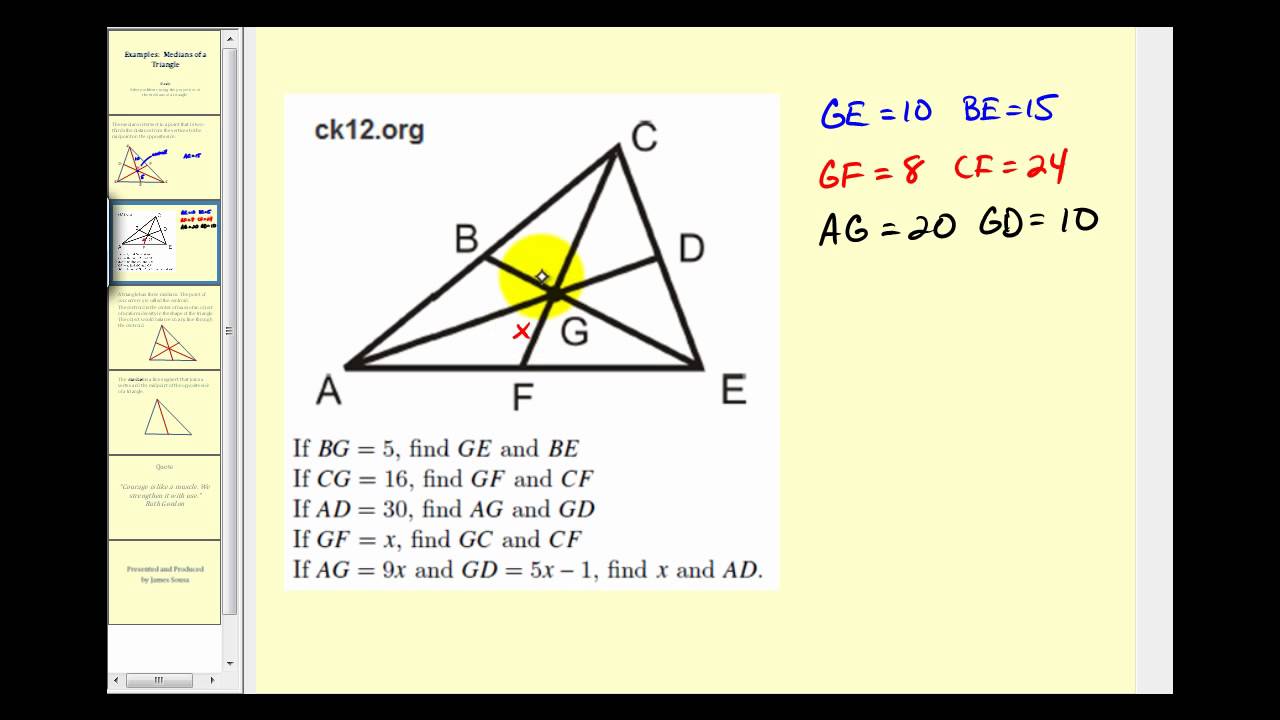
Centroid Ratio Of Medians Sub Segments Some Questions Involving Algebra Solving Segmentation Algebra



